Оценка размеров объекта по параметрам распределения фотоотсчетов
Основная идея
При локации объектов, находящихся на расстоянии нескольких сотен километров от лазерной локационной системы, интенсивность рассеянного излучения в окрестности приемной оптической системы оказывается малой. Результатом воздействия этого излучения на фотодетектор является формирование на его выходе импульсов тока, которые можно рассматривать как отдельные равноценные события – фотоотсчеты.
Закон распределения вероятности 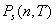 регистрации n сигнальных фотоотсчетов в интервале времени
регистрации n сигнальных фотоотсчетов в интервале времени 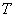 зависит от размеров облученной части поверхности объекта. Число степеней свободы
зависит от размеров облученной части поверхности объекта. Число степеней свободы 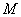 поля рассеянного излучения в первом приближении определяется отношением площади когерентности излучения
поля рассеянного излучения в первом приближении определяется отношением площади когерентности излучения 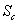 в окрестности приемной апертуры к площади этой апертуры
в окрестности приемной апертуры к площади этой апертуры 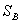 :
:
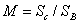 .
.
Рассеяние излучения поверхностями большинства реальных объектов подчиняется закону Ламберта, поэтому
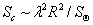 ,
,
где 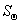 – площадь проекции поверхности объекта
– площадь проекции поверхности объекта 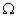 на плоскость, перпендикулярную вектору наблюдения объекта. Если среднее число фотоотсчетов
на плоскость, перпендикулярную вектору наблюдения объекта. Если среднее число фотоотсчетов 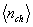 , обусловленных воздействием на фотодетектор фонового излучения, много меньше, чем среднее число фотоотсчетов
, обусловленных воздействием на фотодетектор фонового излучения, много меньше, чем среднее число фотоотсчетов 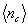 , обусловленных воздействием на него рассеянного поверхностью объекта излучения, то
, обусловленных воздействием на него рассеянного поверхностью объекта излучения, то
 .
.
Определив начало интервала времени 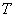 , в пределах которого регистрируетcя импульс рассеянного излучения, на основании экспериментальных наблюдений можно установить вид распределения
, в пределах которого регистрируетcя импульс рассеянного излучения, на основании экспериментальных наблюдений можно установить вид распределения 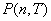 и оценить число степеней свободы поля рассеянного излучения
и оценить число степеней свободы поля рассеянного излучения 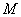 . Зная условия локации объекта, по полученному значению
. Зная условия локации объекта, по полученному значению 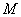 можно судить о характере рассеяния излучения поверхностью объекта, габаритные размеры которого известны, или получить оценку радиуса
можно судить о характере рассеяния излучения поверхностью объекта, габаритные размеры которого известны, или получить оценку радиуса 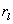 диффузно рассеивающего круга (плоской модели
диффузно рассеивающего круга (плоской модели 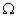 ), статистические характеристики рассеянного поля излучения которого эквивалентны характеристикам поля излучения, рассеянного
), статистические характеристики рассеянного поля излучения которого эквивалентны характеристикам поля излучения, рассеянного 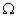 . Корректное определение величины
. Корректное определение величины 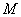 требует обеспечения репрезентативности экспериментальной выборки фотоотсчетов. Необходимое для этого число циклов локации определяется из условий распространения излучения и требуемой погрешности оценки размеров объекта.
требует обеспечения репрезентативности экспериментальной выборки фотоотсчетов. Необходимое для этого число циклов локации определяется из условий распространения излучения и требуемой погрешности оценки размеров объекта.
Результаты проведенных экспериментов подтвердили эффективность метода. Регистрация излучения, рассеянного вращающимся матовым диском и прошедшего через сменную диафрагму известного диаметра, осуществлялась фотоэлектронным умножителем. Быстродействующий аналого-цифровой преобразователь и сопряженная с ним ПЭВМ обеспечивают регистрацию отсчетов амплитуд сигналов, пропорциональных числам фотоотсчетов, зарегистрированных в интервале наблюдения 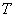 . В результате статистической обработки полученных отсчетов амплитуд сигналов построены распределения чисел зарегистрированных фотоотсчетов и определены числа пространственных степеней свободы поля излучения, которые соответствуют размерам физической модели объекта.
. В результате статистической обработки полученных отсчетов амплитуд сигналов построены распределения чисел зарегистрированных фотоотсчетов и определены числа пространственных степеней свободы поля излучения, которые соответствуют размерам физической модели объекта.
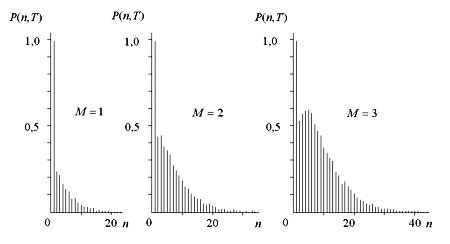
Экспериментально полученные распределения фотоотсчетов
Математическое моделирование реализаций фототока
на выходе фотоэлектронного умножителя
Перспективным направлением развития методов обработки сигналов в импульсной лазерной локации, обеспечивающих измерение расстояний до удаленных объектов с высокой точностью и их распознавание, является анализ отсчетов реализаций сигнала на выходе фотодетектора.
Для анализа потенциальных возможностей различных методов обработки и определения совокупности требований к техническим средствам регистрации и преобразования сигналов наиболее эффективно применение имитационного моделирования их реализаций на выходе фотодетектора, учитывающего квантовый характер регистрации излучения.
Фотодетектирование является квантовомеханическим процессом: результатом воздействия на фотодетектор излучения с постоянной интенсивностью является формирование потока первичных фотоэлектронов, причем число 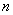 регистрируемых в интервале наблюдения
регистрируемых в интервале наблюдения 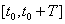 фотоэлектронов подчиняется закону Пуассона:
фотоэлектронов подчиняется закону Пуассона:
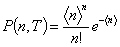 ,
,
где 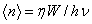 – среднее в этом интервале число фотоэлектронов,
– среднее в этом интервале число фотоэлектронов, 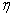 – квантовая эффективность фотодетектора,
– квантовая эффективность фотодетектора, 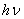 – энергия кванта,
– энергия кванта, 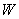 – энергия регистрируемого излучения:
– энергия регистрируемого излучения:
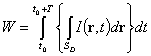 ,
,
где 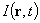 – интенсивность излучения в различных точках поверхности
– интенсивность излучения в различных точках поверхности  фотодетектора, определяемых радиус-вектором r. Так как
фотодетектора, определяемых радиус-вектором r. Так как 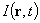 является случайной функцией времени,
является случайной функцией времени,
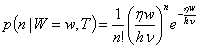 ,
,
где 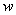 – реализация случайной величины
– реализация случайной величины 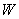 энергии оптического сигнала. Основываясь на полуклассическом методе Манделя установления связи между статистическими свойствами оптических полей и соответствующих отсчетов фотоэлектронов, получаем
энергии оптического сигнала. Основываясь на полуклассическом методе Манделя установления связи между статистическими свойствами оптических полей и соответствующих отсчетов фотоэлектронов, получаем
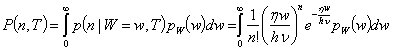 ,
,
откуда следует, что в общем случае распределение 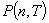 существенно отличается от пуассоновского. Наблюдаемый на выходе фотоэлектронного умножителя процесс
существенно отличается от пуассоновского. Наблюдаемый на выходе фотоэлектронного умножителя процесс  представляет собой суперпозицию одноэлектронных импульсов:
представляет собой суперпозицию одноэлектронных импульсов:
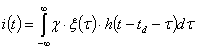 ,
,
где 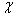 – амплитуда одноэлектронного импульса, являющаяся случайной величиной вследствие флуктуаций коэффициента умножения, а
– амплитуда одноэлектронного импульса, являющаяся случайной величиной вследствие флуктуаций коэффициента умножения, а
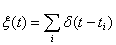 ,
,
– реализация случайного потока первичных фотоэлектронов, формирующихся в моменты времени 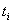 ,
, 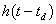 – функция импульсного отклика динодной системы и выходной цепи фотоэлектронного умножителя на единичное событие – формирование первичного фотоэлектрона. Величина
– функция импульсного отклика динодной системы и выходной цепи фотоэлектронного умножителя на единичное событие – формирование первичного фотоэлектрона. Величина 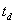 соответствует временному интервалу между моментом времени
соответствует временному интервалу между моментом времени 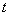 формирования первичного фотоэлектрона и моментом времени достижения максимума одноэлектронного импульса.
формирования первичного фотоэлектрона и моментом времени достижения максимума одноэлектронного импульса.
Таким образом, моделирование реализаций выходного тока  фотоэлектронного умножителя заключается в формировании
фотоэлектронного умножителя заключается в формировании  реализаций
реализаций 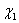 ,…,
,…,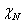 случайной величины
случайной величины 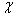 для всех
для всех  одноэлектронных импульсов, регистрируемых в интервале времени
одноэлектронных импульсов, регистрируемых в интервале времени 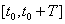 .
.
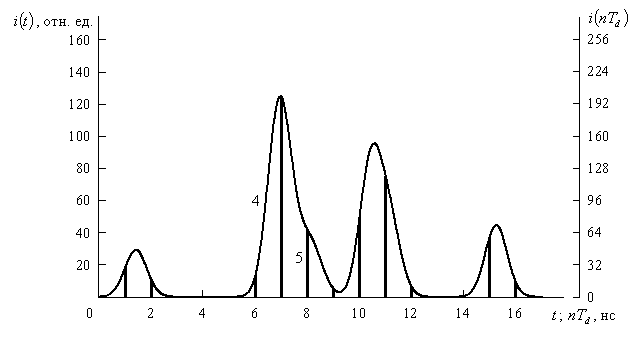 Реализация отсчетов импульса фототока
Реализация отсчетов импульса фототока
при регистрации импульса излучения гауссовской формы длительностью 5·10-9 с
Проведенные исследования показали, что в одном цикле локации удаленного объекта в результате регистрации отсчетов реализации огибающей импульса тока на выходе фотоэлектронного умножителя и последующего их анализа достижима и технически реализуема погрешность измерения расстояния 0,05…0,1 м.
Подробнее
- Себекин Ю.Н., Бурый Е.В., Загидуллин Р.Ш. Оценка эффективности использования пачки импульсов в оптических локационных системах // Алгоритмы обработки сигналов в радиоэлектронных устройствах: Сб. статей / Под ред. И.Б. Федорова. – М.: Изд.–во МГТУ, 1989.
- Бурый Е.В., Смирнова Ю.Л. Влияние квантового характера регистрации излучения малой интенсивности на погрешность измерения расстояний в импульсной лазерной локации // Квантовая электроника, 2004. – Т. 34, № 12.


 English
English