Оценка угловых размеров объекта
по параметрам корреляционной функции
рассеянного лазерного излучения

 

Основная идея

Характеристики поля излучения в окрестности приемника лазерной локационной системы зависят как от параметров излучения передатчика и трассы распространения излучения, так и от геометрии и отражательных свойств поверхности лоцируемого объекта. Результатом рассеяния когерентного лазерного излучения поверхностью объекта является формирование развитой интерференционной картины в окрестности регистрации излучения, называемой спекл-структурой.

В случае, когда получить изображение объекта приемлемого качества в силу дифракционных ограничений невозможно, для оценки углового размера объекта можно применять метод анализа параметров корреляционной функции поля рассеянного излучения. Когда расстояние до объекта существенно превышает его максимальный поперечный размер, случайное поле интенсивностей является однородным и, в большинстве практических случаев, стационарным. Корреляционная функция этого поля имеет вид

,

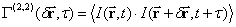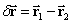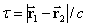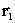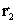где , , и – радиус-векторы, определяющие положения фотодетекторов в системе координат наблюдения, 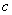– скорость света.

В качестве информативного параметра корреляционной функции можно использовать расстояние 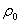между ее главным максимум и первым локальным минимумом, пропорциональное угловому размеру лоцируемого объекта. В классическом методе корреляции интенсивностей Хенбери Брауна и Твисса оценка корреляционной функции 4-го порядка поля излучения измеряется как взаимная корреляционная функция двух случайных процессов:

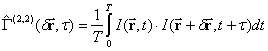
где 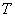– интервал наблюдения. По полученной оценке 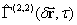определяется искомое значение параметра 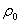и вычисляется величина 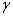. Скорость сходимости интеграла зависит от условий наблюдения объекта, поэтому требуемое время наблюдения 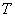может оказаться неприемлемо большим – от нескольких десятков минут до нескольких часов. Поэтому для однородного случайного поля интенсивностей нами предложено получать мгновенную оценку корреляционной функции излучения путем вычисления пространственной свертки интенсивностей:

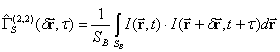
где 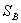– выбранное пространство наблюдения в плоскости наблюдения. Для плоского объекта, как правило, 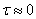. При локации плоских объектов, имеющих ось симметрии, можно использовать одномерную свертку:

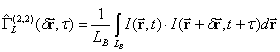
где 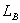– произвольно выбранный отрезок на плоскости наблюдения, 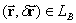. Если для поля интенсивностей справедлива эргодическая теорема по отношению к операции одномерной свертки, то принципиально возможно измерение параметра 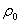в одном цикле локации при достаточной длине .

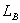Для объекта с ламбертовской рассеивающей поверхностью

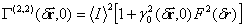
где 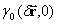– степень когерентности излучения, рассеянного объектом, в свободной от турбулентности среде, 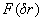– степень когерентности сферической волны в условиях турбулентности. В случае сильной турбулентности 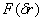является монотонно убывающей функцией, поэтому корреляционная функция обращается в нуль при тех же значениях 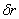, что и 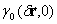. Таким образом, оценка параметра 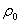, построенная по отсчетам корреляционной функции излучения, распространявшегося через атмосферный канал с выраженной турбулентностью, является асимптотически несмещенной.

Проведенные эксперименты показали, что результирующая погрешность измерения параметра 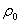может достигать сотых долей шага размещения фотодетекторов, чему соответствует интервал значений 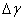10-7…10-8 рад для значений 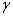10-4…10-5 рад. В результате проведенных экспериментов установлено, что математические ожидания оценок 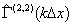совпадают с теоретически рассчитанными с погрешностью не более 5%.

   


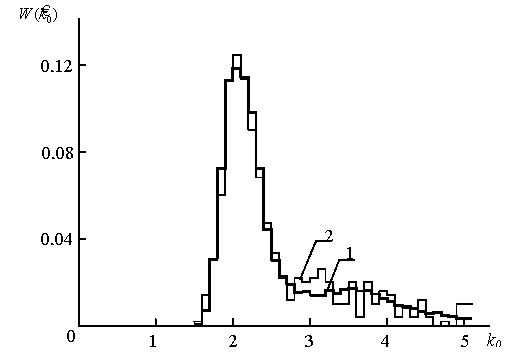
Гистограммы оценок параметра 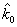корреляционной функции 4-го порядка
 поля рассеянного излучения, полученные методом дискретной одномерной свертки
в результате численного моделирования (1) и экспериментально (2)

 

Основной недостаток метода – необходимость регистрации интенсивности поля рассеянного излучения в окрестностях нескольких точек пространства, расстояние между которыми должно быть меньше радиуса корреляции рассеянного излучения. Главное преимущество – возможность получения высокоточных оценок не только угловых, но и линейных размеров объектов в случае их импульсной локации.

 

Визуализация лоцируемых объектов

<<- Нажмите, чтобы показать раздел ->>
<<- Нажмите, чтобы скрыть раздел ->>

 

Известно, что изображение наблюдаемого объекта не только содержит наибольшее количество информации о нем, но и позволяет интерпретировать результаты наблюдений даже тогда, когда качество изображения оказывается невысоким.

В тех случаях, когда не удается получить изображение объекта хорошего качества в силу дифракционных ограничений приемной оптической системы или в результате распространения излучения через среду с развитой турбулентностью, можно реконструировать часть его поверхности, используя совокупность оценок угловых размеров этого объекта.

Применение метода одномерной дискретной свертки отсчетов поля интенсивностей позволяет оценивать величины отсчетов сечения корреляционной функции плоскостью, образующей угол 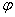с плоскостью регистрации излучения.

В основе реконструкции лежит возможность измерения угловых размеров 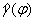различных сечений контура объекта 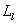. Образ 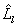контура может быть построен в результате поиска пересечения на модельной плоскости 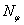полос шириной 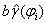, 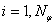( 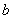– масштабный коэффициент) с осевыми линиями  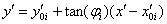. Пересечение двух полос, для которых выполняется условие

.

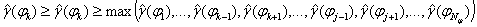при 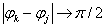, определяет область возможного решения . Параметры 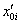и 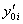, в общем случае отличные от нуля, могут быть найдены вариационным методом для остальных 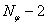полос при удовлетворении условия принадлежности всех точек пересечений границ полос области, ограниченной 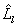. Результатом поиска решения будет определение образа контура 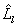– некоторого выпуклого многогранника, принципиально имеющего хотя бы одну ось симметрии, угловые размеры которого с точностью до постоянного множителя совпадут с габаритными угловыми размерами лоцируемого объекта.

Установлено, что реконструированный по линии первого минимума корреляционной функции контур 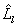аппроксимирует 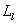с малой погрешностью, когда 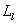представляет собой окружность или эллипс. В остальных случаях возникают ошибки при определении формы 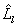и его ориентации относительно системы координат наблюдения. Отсюда следует, что в тех случаях, когда 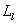не обладает свойством осевой симметрии, сопоставление реконструированного контура 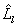с множеством контуров 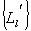, рассчитанных для некоторой совокупности моделей объектов, позволит определить подмножество 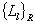моделей (и, соответственно, подмножество контуров 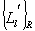), корреляционные функции полей излучения которых можно считать соответствующими зарегистрированной корреляционной функции. Если априорные сведения о форме поверхности объекта отсутствуют, при проведении последовательных во времени циклов локации можно оценить изменение ориентации объекта относительно системы координат наблюдения по изменению ориентации  .

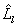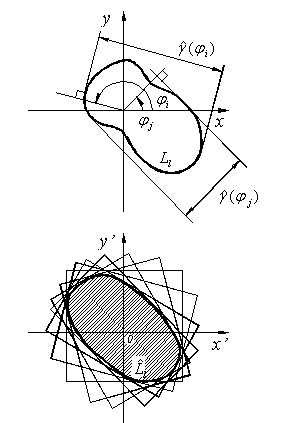
Реконструкция по параметрам КФ 4-го порядка
контура объекта по совокупности оценок его угловых размеров

 

Результаты реконструкции контуров плоских объектов:
сплошная линия – результат реконструкции, пунктир – контур объекта

 

Подробнее

  1. Бурый Е.В., Митрофанов А.Л. Оценка функции когерентности 4–го порядка методом пространственной свертки и перспективы ее применения в лазерных информационных системах // Квантовая электроника. – 1996. – Т. 23. – №5.
  2. Бурый Е.В., Митрофанов А.Л. Точность измерения углового радиуса объекта по оценкам функции когерентности четвертого порядка в оптически однородных и турбулентных средах // Квантовая электроника. – 1997. – Т. 24. – № 1.
  3. Бурый Е.В., Рождествин В.Н. Перспективы развития методов получения информации о форме объектов в лазерных локационных системах и способы ее использования // Вестник МГТУ им. Баумана. Приборостроение. – 1998. – Спец. вып.
  4. Бурый Е.В., Косыгин А.А. Оценка габаритных угловых размеров объектов и реконструкция их контуров по параметрам корреляционной функции излучения 4-го порядка // Квантовая электроника, 2004. – Т. 34, № 10.