Estimation of an object angular dimensions by correlation function
of scattered laser radiation parameters
Essence
Radiation characteristics in laser location system detector area depend on transmitter parameters and radiation propagation channel. It also depends on surface shape and reflectance of located object. Fringe pattern in intensity detection area, named speckle-structure, is a result of coherent laser radiation scattering by objects surface.
Sometimes it is impossible to get objects image because of diffraction restrictions. In this case scattered intensity field correlation function parameters analysis method can be used. When distance to object significantly exceeds its maximum transverse dimension random intensity field is uniform and stationary in most practical cases. Correlation function of such field is
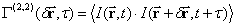 ,
,
where  ,
, 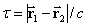 ,
, 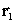 and
and 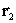 – are radius-vector, which determines photodetector disposition in observation frame of reference,
– are radius-vector, which determines photodetector disposition in observation frame of reference, 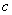 – velocity of light.
– velocity of light.
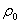 is distance between main maximum of correlation function and first local minimum. It can be used as informative parameter, which is proportional to located object angular dimensions. There is intensity correlation Hanburry-Brown and Twiss classic method. Estimation of 4th order correlation function is evaluated as inter correlation function of two random processes:
is distance between main maximum of correlation function and first local minimum. It can be used as informative parameter, which is proportional to located object angular dimensions. There is intensity correlation Hanburry-Brown and Twiss classic method. Estimation of 4th order correlation function is evaluated as inter correlation function of two random processes:
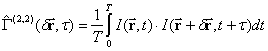
where 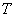 – is observation interval. By obtained
– is observation interval. By obtained 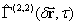 estimates of
estimates of 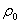 parameter is determined and value
parameter is determined and value 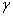 is counted. Integral rate of convergence depends on object observation conditions, thus observation time
is counted. Integral rate of convergence depends on object observation conditions, thus observation time 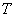 required could be unacceptable long – from some dozens of minutes till some hours. Therefore for uniform random intensity field we propose to obtain instantaneous radiation correlation function estimation by intensity spatial convolution:
required could be unacceptable long – from some dozens of minutes till some hours. Therefore for uniform random intensity field we propose to obtain instantaneous radiation correlation function estimation by intensity spatial convolution:
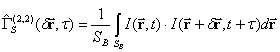
where 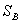 – is selected area in observation plain. For plain object we can assume
– is selected area in observation plain. For plain object we can assume 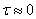 . In case of plain objects with axis of symmetry we use one-dimensional convolution:
. In case of plain objects with axis of symmetry we use one-dimensional convolution:
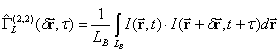
where  – is randomly selected segment in observation plain,
– is randomly selected segment in observation plain,  . If ergodic theorem in one-dimensional convolution procedure for intensity field is valid, than
. If ergodic theorem in one-dimensional convolution procedure for intensity field is valid, than  parameter measuring in one location cycle under sufficient
parameter measuring in one location cycle under sufficient 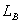 length is possible on principal.
length is possible on principal.
For object with lambert surface
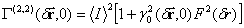
where 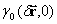 – is objects scattered radiation coherence degree in turbulence free area,
– is objects scattered radiation coherence degree in turbulence free area, 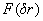 – is spherical wave coherence degree in turbulence conditions. In case of advanced turbulence
– is spherical wave coherence degree in turbulence conditions. In case of advanced turbulence 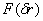 is monotonically decreasing function, therefore correlation function makes vanish in the same valuesявляется монотонно убывающей функцией, поэтому корреляционная функция обращается в нуль при тех же значениях
is monotonically decreasing function, therefore correlation function makes vanish in the same valuesявляется монотонно убывающей функцией, поэтому корреляционная функция обращается в нуль при тех же значениях 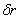 , as
, as 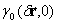 . Thus, if
. Thus, if 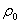 , parameter estimation is counted by estimates of radiation correlation function propagated through atmospheric channel with advanced turbulence, it is asymptotically unbiased.
, parameter estimation is counted by estimates of radiation correlation function propagated through atmospheric channel with advanced turbulence, it is asymptotically unbiased.
Experiments being carried out proves that 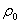 parameter estimation total error can achieve hundredth of photodetector pitch location, e.g. value interval
parameter estimation total error can achieve hundredth of photodetector pitch location, e.g. value interval 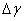 10-7…10-8 radian for
10-7…10-8 radian for 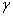 in 10-4…10-5 radian. Experimentally determined, that mathematical expectation of
in 10-4…10-5 radian. Experimentally determined, that mathematical expectation of 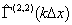 estimates corresponds with theoretically counted one with error low than 5%.
estimates corresponds with theoretically counted one with error low than 5%.
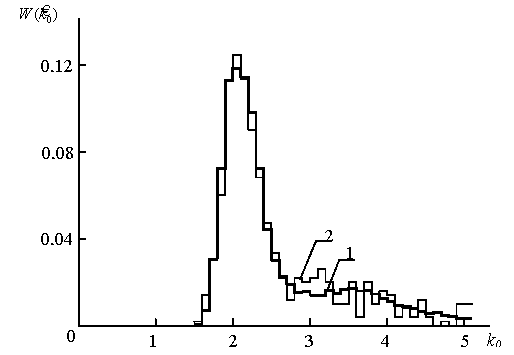
Radiation scattered field 4th order correlation function 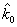 parameter estimates histogram,
parameter estimates histogram,
obtained by discrete spatial convolution after numerical modeling (1) and experimentally (2).
Main method disadvantage is that it is necessary to register scattered radiation intensity field in several different points, with distance between them less than scattered radiation correlation radius. Main advantage is ability to estimate not only angular, but object linear dimensions in case of counting location with high accuracy.
Located objects visualization
It is all known, that image of located object has not only maximum information about it, but allows to interpreter observation results even, when image quality is low.
In cases when it is impossible to retrieve good image quality by virtue of receiving optical system diffraction restrictions or because of propagation medium turbulence, it is possible to reconstruct the part of its surface by objects angular dimensions estimates.
Using of intensity field sample one-dimensional discrete convolution allows estimating section of correlation function sample values. Angle between this section and registration plane is 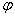 .
.
In the basis of reconstruction is possibility of angle dimensions 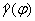 measuring for different object
measuring for different object 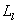 . Contour
. Contour 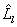 shape could be reconstructed by intersections on model plane
shape could be reconstructed by intersections on model plane 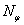 of streaks with bandwidth
of streaks with bandwidth 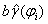 ,
, 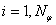 (
(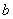 – scale factor) and axis
– scale factor) and axis 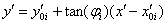 .
.
Two streaks intersection, for which
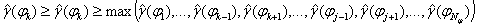 .
.
with 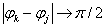 , determine feasible solution area
, determine feasible solution area ![]() . Parameters
. Parameters 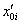 и
и 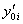 , nonzero in common case, can be found by variational method for another
, nonzero in common case, can be found by variational method for another 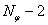 streaks. In this case all points of streaks borders intersection must be in
streaks. In this case all points of streaks borders intersection must be in 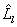 area. As a result we should have estimation of figure shape
area. As a result we should have estimation of figure shape 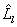 – with angular dimensions equal to located objects overall angular dimensions with some constant factor. This shape is some convex polyhedron, having at least one axis of symmetry principally.
– with angular dimensions equal to located objects overall angular dimensions with some constant factor. This shape is some convex polyhedron, having at least one axis of symmetry principally.
Errors of reconstruction by correlation function first minimum line of contour 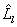 approximate
approximate 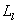 with low errors when
with low errors when 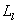 is circle or ellipse. There are errors of shape
is circle or ellipse. There are errors of shape 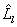 and orientation relative location system estimation in other cases. When
and orientation relative location system estimation in other cases. When 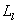 shape isn’t axisymmetric, comparison of reconstructed contour
shape isn’t axisymmetric, comparison of reconstructed contour 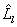 and amount of contours
and amount of contours 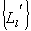 , counted for some aggregate of objects, allow us to determine amount of
, counted for some aggregate of objects, allow us to determine amount of 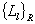 (and corresponded contours
(and corresponded contours 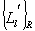 ), with radiation field correlation functions corresponding to registered one. It’s possible to determine objects orientation changes relative location system frame of reference by changes of contour
), with radiation field correlation functions corresponding to registered one. It’s possible to determine objects orientation changes relative location system frame of reference by changes of contour 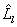 orientation in serial location cycles, if there isn’t any prior information about object surface.
orientation in serial location cycles, if there isn’t any prior information about object surface.
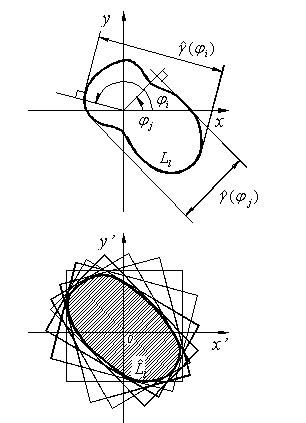
Object contour reconstruction by amount of angular dimensions,
counted by correlation function 4th order.
 Plane objects contour reconstruction results:
Plane objects contour reconstruction results:
firm line – reconstruction result, dotted line – object contour
References
- Бурый Е.В., Рождествин В.Н. Перспективы развития методов получения информации о форме объектов в лазерных локационных системах и способы ее использования // Вестник МГТУ им. Баумана. Приборостроение. – 1998. – Спец. вып.
- E.V. Buryi, A A Kosygin, "Estimate of the angular dimensions of objects and reconstruction of their shapes from the parameters of the fourth-order radiation correlation function", QUANTUM ELECTRON, 2004, 34 (10).
- E.V. Buryi, A.L. Mitrofanov, "Estimate of the fourth-order coherence function by a spatial convolution method and its potential applications in laser information systems", QUANTUM ELECTRON, 1996, 26 (5).
- E.V. Buryi, A.L. Mitrofanov, "Precision of determination of the angular radius of an object from estimates of the fourth-order coherence function in optically homogeneous and turbulent media", QUANTUM ELECTRON, 1997, 27 (1).


 Русский
Русский